Wskazówka:
W tablicach dostępnych na maturze mamy:
POTĘGI I PIERWIASTKI
Niech n będzie liczbą całkowitą dodatnią. Dla dowolnej liczby a definiujemy jej n-tą potęgę:
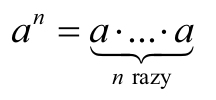
Pierwiastkiem arytmetycznym 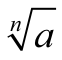 stopnia n z liczby
stopnia n z liczby a ≥ 0
nazywamy liczbę W szczególności, dla dowolnej liczby a zachodzi równość:
Jeżeli a < 0 oraz liczba n jest nieparzysta, to 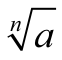 oznacza liczbę
oznacza liczbę b < 0 taką, że bn = a.
Pierwiastki stopni parzystych z liczb ujemnych nie istnieją.
Niech m, n będą liczbami całkowitymi dodatnimi. Definiujemy:
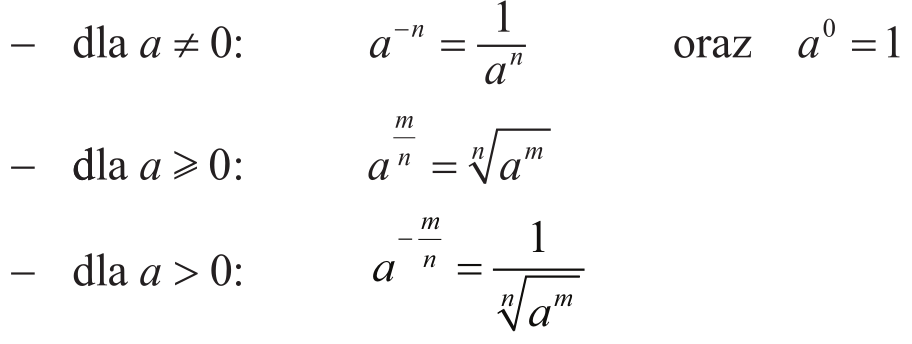
Niech r, s będą dowolnymi liczbami rzeczywistymi. Jeśli a > 0 i b > 0, to zachodzą równości:
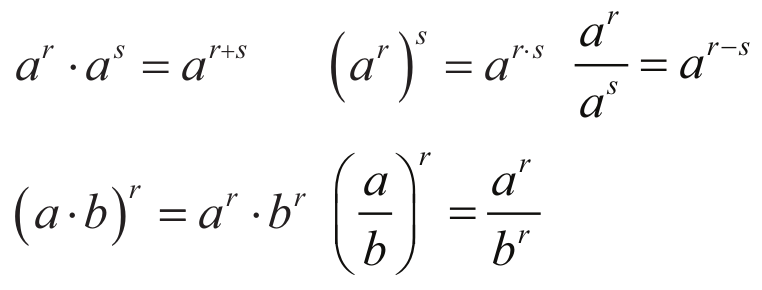
Jeżeli wykładniki r, s są liczbami całkowitymi, to powyższe wzory obowiązują dla wszystkich liczb a ≠ 0 i b ≠ 0.